commbank.eth explained

Foreword/Legal Disclaimer

The following is a detailed explanation of how commbank.eth enables private transfers of assets on public computer networks.

commbank.eth private transfers are currently only enabled for me (meaning only I can deposit real money to the encrypted protocol). As you can probably imagine, the ability to make money vanish in one spot and appear in another is very attractive to those on the other side of the law. It is not impossible to regulate and enforce the same compliance regulations we have in the traditional finance system in commbank.eth, but it is much harder.

Due to this being the current state of things and me valuing not being sent to prison for facilitating crime and/or North Korean money laundering - before private transfers can be open to anyone else, I need to consult with a bunch of very expensive legal people and traditional finance people, and then develop what they advise. If you are one of these people (and/or would be interested in funding this kind of thing), you should reach out to me.

Now that I've done my 'here's why I can't be imprisoned for this' explanation, let us get into the magic of how commbank.eth works.

Context

Any time that you have heard of any cryptocurrency, there is a 99.99% chance that the token being discussed is a public token, often an ERC-20 (or an SPL token on Solana, ASA on Algorand, et cetera). Public here meaning that everybody can see how much every address holds. For example, here's the list of the top 10 holders of the TRUMP memecoin:

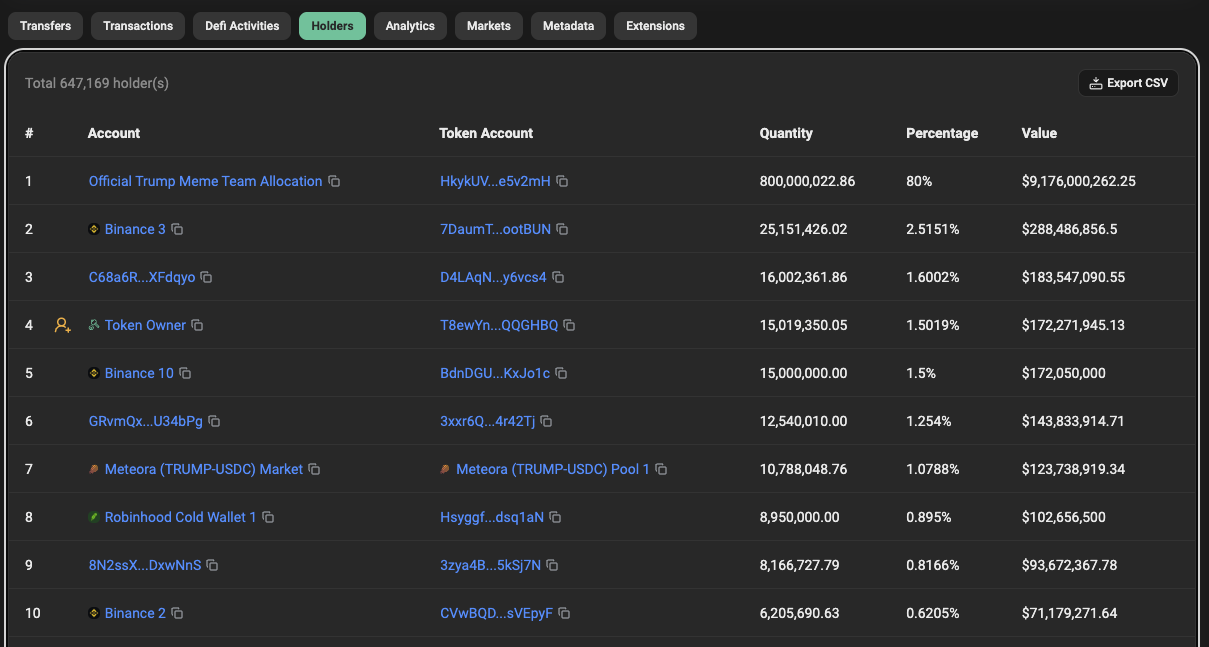
Source: SolScan

This is a noted feature of blockchains/public computers, the fact that everyone can see everything means that accountability and transparency are much more tangible, but it's a terrible feature when compared to the privacy that our traditional banking system offers. If we could all see each others bank balances, the dynamic of society would change pretty drastically, and probably not for the better.

The adoption of blockchain usage to track assets resembles something much larger than the ability to publicly track assets, it represents a movement of our current financial system away from requiring middlemen to facilitate digital payments.

As digital payments have increased exponentially, a handful of very powerful corporations have essentially formed a monopoly on how money moves. These corporations and the fees that they charge are currently quite a political issue in Australia, as it is basically theft. ~1% surcharges on all transactions is not a good outcome for anybody except these corporations, and contributes even more to the ongoing cost of living pressures.

But, not all hope is lost. What if we could have the privacy that we have with the traditional banking system, but on public computers? Where we don't pay a middleman to facilitate the transaction, we just pay for the electricity to process the transaction. This thought experiment is the thesis for commbank.eth.

How do we get privacy, publicly?

Zero Knowledge proofs are a way of proving something is true, without revealing details of how you know it is true. It is a bit mind bending, but I find the Cave example is the best way of explaining it.

Image that you have a circular cave, with the same entry and exit. But, on the far side of the cave is a magic door that requires a secret to open. If someone can go down one side of the cave and come out the other side, it is pretty conclusive evidence that they know the secret password. If you watched someone do this from outside the cave and knew this cave required a secret password to get through, you now know that this person knows the secret password to the door, but you gain no knowledge of what the secret they used is. This is a Zero Knowledge proof, where the prover can verify something is true, without gaining any knowledge about how they know it's true.

Some very smart people have found ways to replicate this same Zero Knowledge gained proving model, while making it arbitrarily programmable. How ZK proofs work is out of scope for this write-up, but it is important to know what they are. Combing ZK Proofs with hash functions is about ~90% of how commbank.eth is able to facilitate private payments.

A hash function is just a function that for a given input, always returns a unique, fixed-length output. A strong hash function is one that has a low collision rate, meaning that for a given input, it is almost a mathematical certainty that it will have a unique output. Hash functions are also normally information losing, or 'trap doors'. Once you hash something, there is no way to go back to the original value you hashed without brute forcing until you find a match.

commbank.eth uses Zero Knowledge proofs to allow its users to prove they know how to recreate publicly recorded and stored hash output values, but without revealing any details about the hash itself, or which hash they're proving.

Deposits

When a user wants to deposit to commbank.eth, they create a note. A note contains:

A note can be committed to by hashing it's contents, i.e.

When the user deposits, the asset and amount that they are depositing is transferred to commbank.eth, with the user providing the note hash too. This note hash is validated with a Zero Knowledge proof, which verifies that the note_hash does actually contain the amount and asset publicly deposited, or the transaction fails.

If the users proof is valid, their note hash is added as a leaf to the commbank.eth Merkle Tree. A Merkle Tree is a very handy data structure, it is a way of expressing a lot of data in a single hash. It works by hashing (often) pairs, level by level, until the top level is reached. This top level is called the root hash, and can only be created by recreating all of the hashes that came before it.

Transfers

A transfer in commbank.eth occurs when at least 1 note is spent, and at least 1 note is created.

Say Alice has a Note A with a value of $10. She wishes to send Bob $6. To do this, she takes her Note A as an input note, and creates 2 output notes, one for $6 belonging to Bob, and one for $4 to herself as change. The most important part of the transfer process is ensuring that the sum of asset inputs = the sum of asset outputs. For each input note, Alice also proves:

Alice's input notes are marked as spent by recording their nullifier. In commbank.eth's case - the nullifier hash is given by:

This nullifier property makes double spending of notes impossible, as for a given note_hash there is only one nullifier_hash output.

Withdrawals

Withdrawals are the exact same as transfers, but they do not create any output notes. The sum of the input notes must equal the sum of the withdrawal amount, and the nullifiers are recorded just the same as transfers. If the withdrawal proof is valid, the exit amount is transferred to the address that the user specifies.

Demonstration Transactions

commbank.eth v0.1 is currently deployed on ethereum mainnet at commbank.eth. I was able to complete a private transaction from one account to another, and here's the receipts.

First, I deposited 5 USDC, with an input note hash of 0x8ddbc096f6b664b4112cd1f19f2be1dcf7df7bdc594eb1baeba384570b3dfe16 in this transaction.

Next, in this transaction, I privately transferred another account I control 2 USDC, meaning I created 2 new note hashes. One for the transaction of 2 USDC, and the other for the 'change' note (3 USDC).

Finally, as the recipient of the 2 USDC note hash, I was able to withdraw my 2 USDC back to an unencrypted asset, which happened in this transaction,

If not for me revealing the details of these transactions (and if I wasn't the only account interacting with commbank.eth), all of the details of my transfer of 2 USDC would be private.

Conclusion

If you've made it this far, thanks for reading. Follow me on twitter for updates on the project, and be sure to check out the codebase if you're into that kind of thing.

cheers 🤙